Ease-In-Out Tween

Introducing Ease-In-Out Tween

Description

This article is a continuation from the ../ease-out-tween article. We will present the graphic plot of the function, update the code, and demonstrate the working animation.

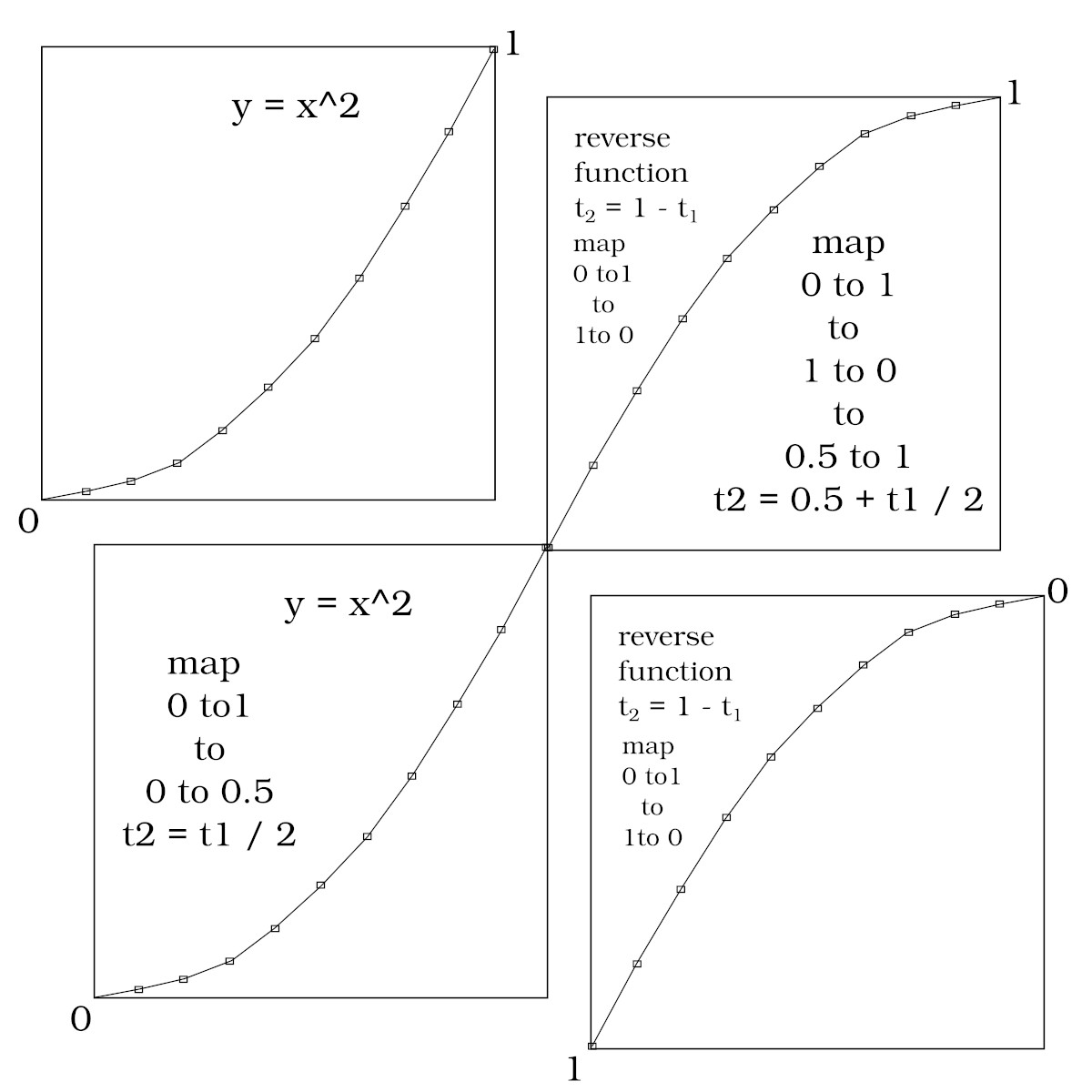
We will build on top of the Ease-In and Ease-Out code base. We will achieve our Ease-In-Out tween by running Ease-In the first half way and then Ease-Out the last half way. To that end, we must map Ease-In to 0 to 0.5 and similarily our Ease-Out to 0.5 to 1. Since our Ease-Out function is the same parabola function in reverse as the Ease-In function, they will intersect and line up smoothly in the middle as we will see in our graphical plot.

Review

Since we will need many layers of mapping functions we will review our layers thus far before beginning walking through the data along the way:

Review no tween algorithm

REF paragraph 1: ../raf-queue

We animated the margin-left property of a 20px div inside 300px container from 0 to 280px. We ignored the raf elapsed time argument value. We add the property "this.speed = 1px;" to our margin-left property. We break out once margin-left reaches the limit 280px.

1. initialization: margin-left = 0;

2. incrementation: margin-left += this.speed;

this.speed is 1px for the first div, 2px for second, ...

Data: 0,1,2,3, ... 280px

BREAK OUT: if ( left_margin > 280)

Review linear tween algorithm

REF paragraph 1: ../linear-tween

We animated the margin-left property of a 50px div inside 300px container from 0 to 250px.

Our algorithm begins with a time value initialized to zero. It is increment on each frame by the elapsed time between frames.

1. current time initialization: ct = 0;

2. current time incrementation: ct += et;

et stands for elapsed time;

Data: 0, 30, 60, ... ~8250

3. left_margin = ct * right_end_point / time_interval

left_margin = ct * 250 / 8250

linear map function x-axis 0 to 1, y-axis 0 to 250

BREAK OUT: if ( left_margin > 249)

Review Ease-In algorithm

REF paragraph 1: ../ease-in-tween

From here on forward we changed our end points to 50 to 200px so our left end point was not 0 and matching our mapping left end point because that would have been too easy and have hidden any errors in our formulations and programming at that end point.

1. ct = 0;

2. ct += et;

Data: 0, 30, 60, ... ~8250

3. param_t = ct / interval ;

Data: 0, 0.1, 0.2, 0.3, 0.4, 0.5, ... 1

4. param_t = parabola( param_t );

Data: 0, 0.03, 0.08, 0.1, 0.3, 0.5, ... 1

Notice that the data is closer together on the left end or 0 end gradually widenning.

5. left_margin = param_t * 150 + 50

linear map x-axis 0 to 1, y-axis 50 to 200

BREAK OUT: if ( left_margin > 199)

Review Ease-Out algorithm

REF paragraph 1: ../ease-out-tween

1. ct = 0;

2. ct += et;

3. param_t = ct / interval

Data: 0, 0.1, 0.2, 0.3, 0.4, 0.5, ... 1

4. param_t = reverse( param_t )

Data: 1, 0.9, 0.8, 0.7, 0.6, 0.5, ... 0

5. param_t = parabola( param_t )

Data: 1, 0.96, 0.93, ... 0.15, 0.1, 0.06 0.03 ,0

Notice by reversing the data the 1 end becomes the left end and we were able to bring the data closer together on the 1 end instead of the 0 end. Next we will want to reverse it again so we have an interval of [0,1] instead of [1,0].

4. param_t = reverse( param_t )

5. left_margin = param_t * 150 + 50

BREAK OUT: if ( left_margin > 199)

Review Ease-In-Out algorithm

See Final Notes at the bottom of this article.

Audience

You are a web programmer interested in gaining insight into programming animations from scratch.

Demo - Ease-In-Out

View the plot of the basic parabola function leading into the reverse of the same parabolic function. So we have to map the forward parabola function 0 to 1 to 0 to 0.5. Then we have to map the forward parabolic function to the reverse parabolic, then map the reverse parabolic from to 0.5 to 1.

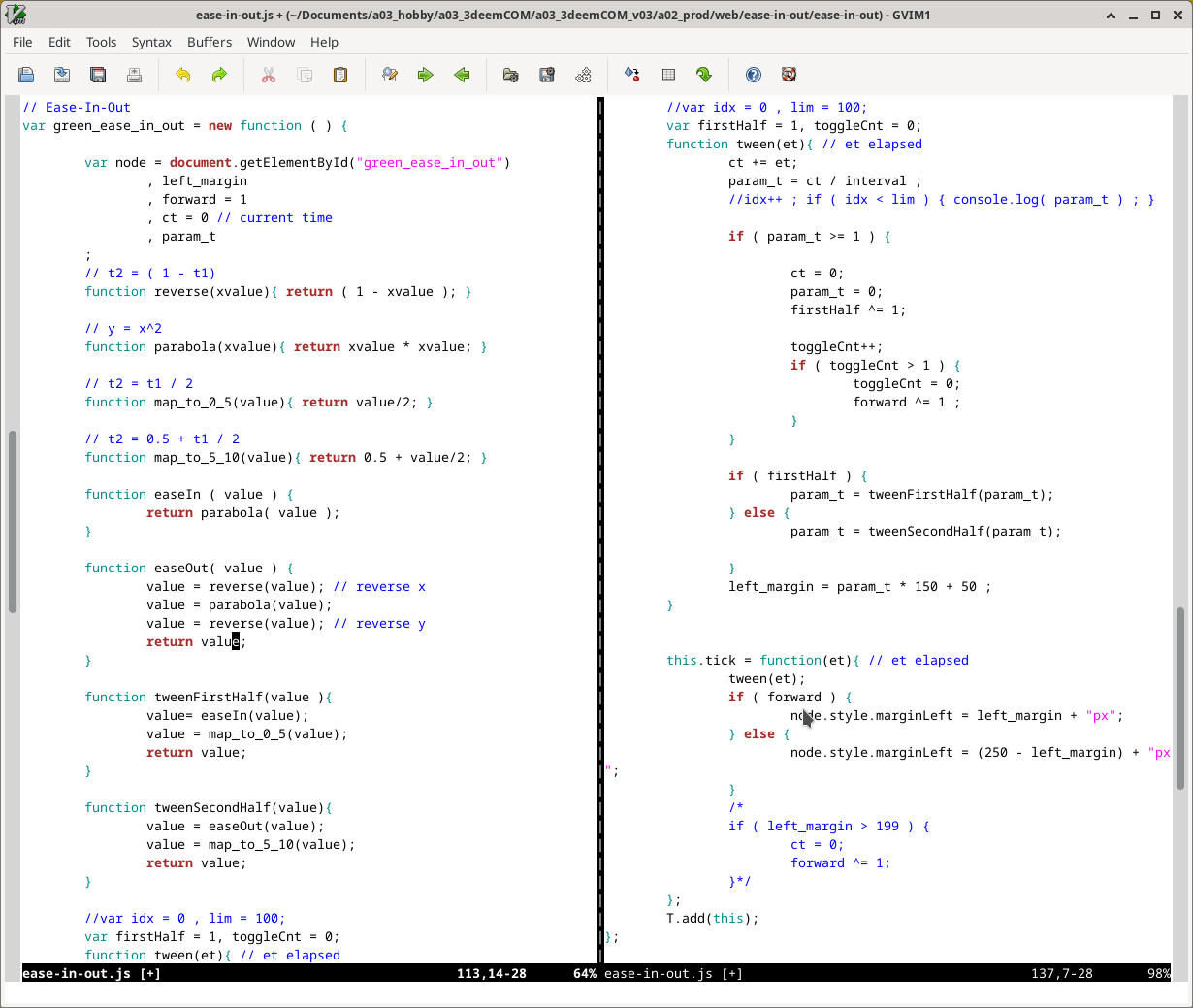
Incorporating the reversed parabola tween function into our animation programming starts with the Ease-In tween programming. With the Ease-In tween, we first calculate the normalized time value, then we run the parabola function, and then normalized linear function. For Ease-out tween'ing, we will again first calculate the normalized time value, then reverse it which will reverse the x-axis, then run the parabola function, then reverse it again which will reverse the y-axis and finally fun the normalized linear function.

demo in it's own page: ./ease-in-out

css file link: ./ease-in-out/ease-in-out.css

raf Timer file link: ./ease-in-out/Timer.js

js file link: ./ease-in-out/ease-in-out.js

Notice we had to move out reverse direction "forward" toggle logic from the tick() method to the tween() method. Instead of checking the margin-left property has reached the end, we checked that the param_t property reached 1 twice before any mapping functions are applied.

Conclusion

The Ease-In-Out function can be achieved by a half-piece wise combination of an Ease-In function mapped from [0,1] to [0,0.5] plus the same Ease-In function reversed resulting in an Ease-Out function, mapped from [0,1] to [0.5,1].

Final Notes - Review Ease-In-Out

In this article, we organized the mapping layers in our code. Review the layers is hardly needed now. But for the sake of completeness:

1. ct = 0;

2. ct += et;

3. param_t = ct / interval

We split our programming logic into 4. A) Ease-In and 4. B) Ease-Out.

Notice param_1 goes from 0 to 1 to the middle of the animation and then again 0 to 1 from the middle to the end. That is why we needed to move the forward/reverse code logic from the tick() method to the tween() method.

4.A) Ease-In

Ease-In followed by mapping 0 to 1 to 0 to 0.5: t2 = t1 / 2

4.B) Ease-In

Ease-Out followed by mapping 0 to 1 to 0.5 to 1: t2 = 0.5 + t1 / 2