Linear Tween'ing

Introducing Linear(constant speed) Tween'ing

Description

The term tween is a playful name for referring to an important animation concept. It is shorthand for the term "in between" which refers to the path points in between two end points of an animation. It is important for improving the visual appeal of our animations. Tween'ing adds style and pizzazz to our animations by easing in or out or both.

Real world motion is not instantaneous, so a motion animation that starts at the top speed will look strange to us even if we do not realize it. Motion that starts slowly and then speeds up to the top speed will look more realistic. Here we will only cover linear tween for instructional purpose. Here we will demonstrate how to formulate tween'ing functions. In the next article we will see easing. When we see easing we will gain full appreciation of the improved visual appeal offered by tween'ing our animations.

Tween'ing in CSS is as simple as adding the keyword "Ease" to a node's css property settings.

REF paragraph 1: w3schools.com/css/css3_transitions.asp

In JavaScript, we need to program tween'ing ourselves manually. We will demonstrate tween'ing in JavaScript.

When designing our animations without tween'ing, we simply increment our property on every frame. Notice that without any tween'ing we have a constant speed animation: ../js-vs-css-animations/demo-raf-timer

We have a linear tween but our code does not use a tween'ing function. We have just the one parameter, the increment amount. For tweening, we use a tween function that requires three parameters: our time interval and the begining and end point values of the property we are animating. Here we will code that linear tween with and without a tween function.

Audience

You are a web programmer interested in gaining insight into programming animations from scratch.

Demo - linear tween

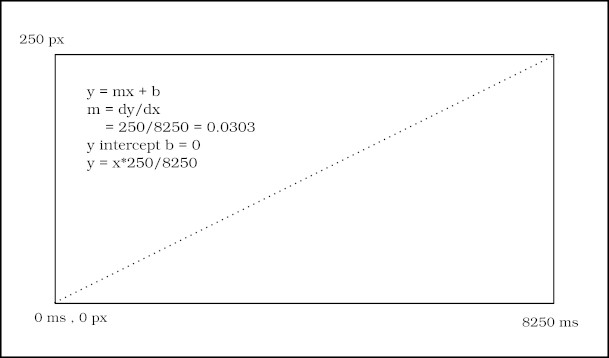
For a constant speed animation we have a flat line function. For the example demonstration, we will use a container div of size 50 by 300px. We will animate a 50 by 50px div's margin-left property from 0 to 250px. So our end points input parameters are 0 and 250px. We will use the speed of 33ms that we find when running raf without any operations: ./elapsed-time. When advancing 1px every 33ms we reach our end point tranversing 250px in 33 x 250 = 8250 ms. So to do the same animation with tween'ing at tween function formulation would be: margin-left = time * 250 / 8250.

Let's verify our calculations by viewing both a non tween'ing demo with a demo of our tween function.

demo in it's own page: ./constant-speed

css file link: ./constant-speed/constant-speed-tween.css

raf Timer file link: ./constant-speed/Timer.js

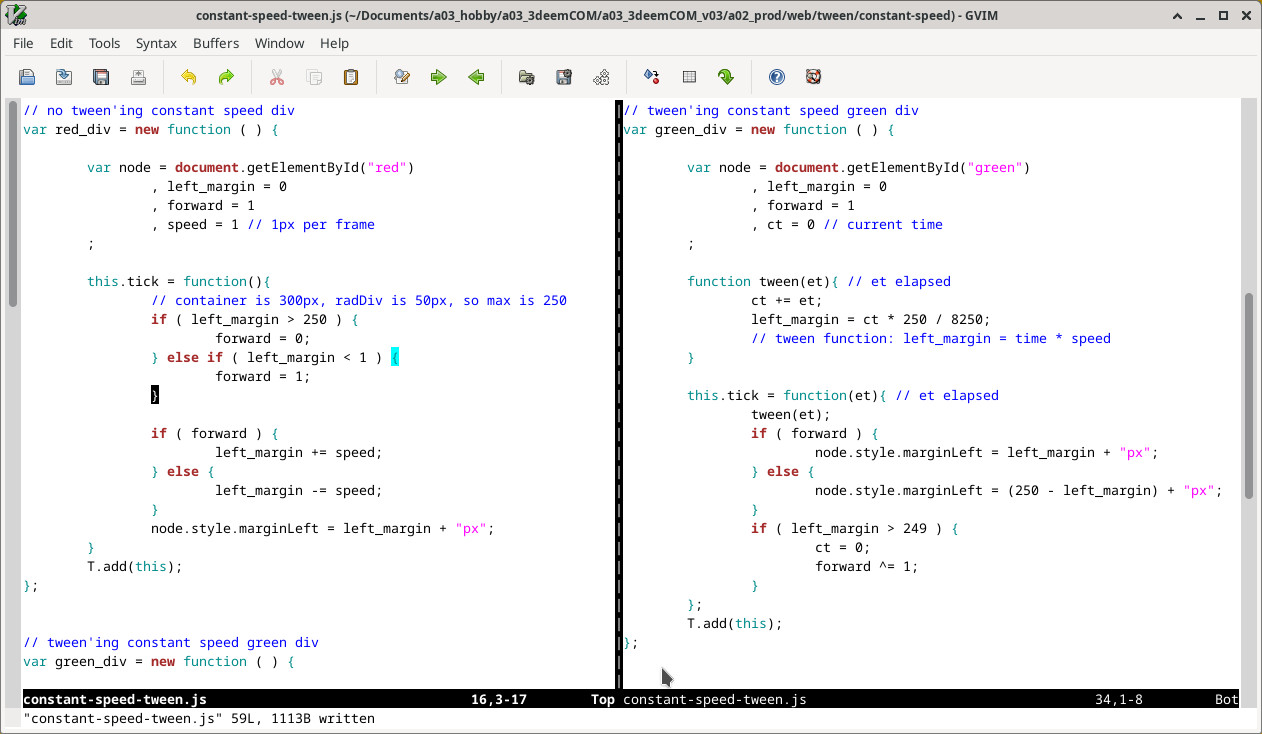
js file link: ./constant-speed/constant-speed-tween.js

Conclusion

Formulating a tween'ing function involves mapping our parameters to a time interval. We mapped incrementing 1px per frame at a framerate of 33 ms per frame to a time interval of 8250 ms.

Normalization

If you research tween'ing you will note that tweens are normalized. Normalization maps a set of end point params to end points 0 to 1. Our current demo animation start at a margin-left property value of zero. A zero start point is a simplified case. In practive we will have to work out cases where the start point is other than zero. So for instructional purposes let's change our animation to go from 50 to 200 instead of 0 to 250. With that change, our time interval will be 33 x 150 = 4950. Then when we normalize we will appreciate the added benefit of normalization which is that our parameters will start from 0 again.

We normalization of our margin-left property as a function of time by introducing a 3rd dummy parameter. This mathematical technique is called parameterization. So to begin let's define our function again:

y(x) = x * (dy/dx) + b // here y represents our margin-left in px and x represents time in ms

Our end points are (0 ms , 50 px) and (4950 ms , 200 px).

dy/dx = 150 / 4950

at x = 0, y = 50 so our y-intercept b = 50

So our function is y = x * ( 15 / 495 ) + 50

Parameterize our function f( y(x) , x ) to a 3rd dummy parameter t as f( y(t) , x(t) ). where t is our normalizer varying from 0 to 1

x(t) = t * dx/dt + b , end points t(0 to 1), x(0 to 4950), dt = 1 , dx = 4950

y(t) = t * dy/dt + b , end points t(0 to 1), y(50 to 200), dt = 1 , dy = 150

EQ.1 | x(t) = t * 4950

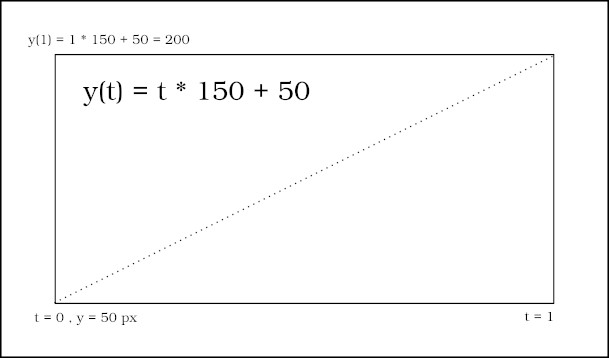
EQ.2 | y(t) = t * 150 + 50

In our code, we will be increment current time ct starting from 0 to 4950 which is x(t). Using EQ.1 we can calculate t = x(t) / 4950. With t we can calculate y(t) which is our margin-left property of interest along our animation interval from 50 to 200 px.

Our margin-left y(t) parameterized tween plot:

Our elapsed time x(t) parameterized tween plot would look the same.

Coding our animation object's tween function to use the above parameterized/normalized equations.

demo in it's own page: ./normalized

css file link: ./normalized/normalized.css

raf Timer file link: ./normalized/Timer.js

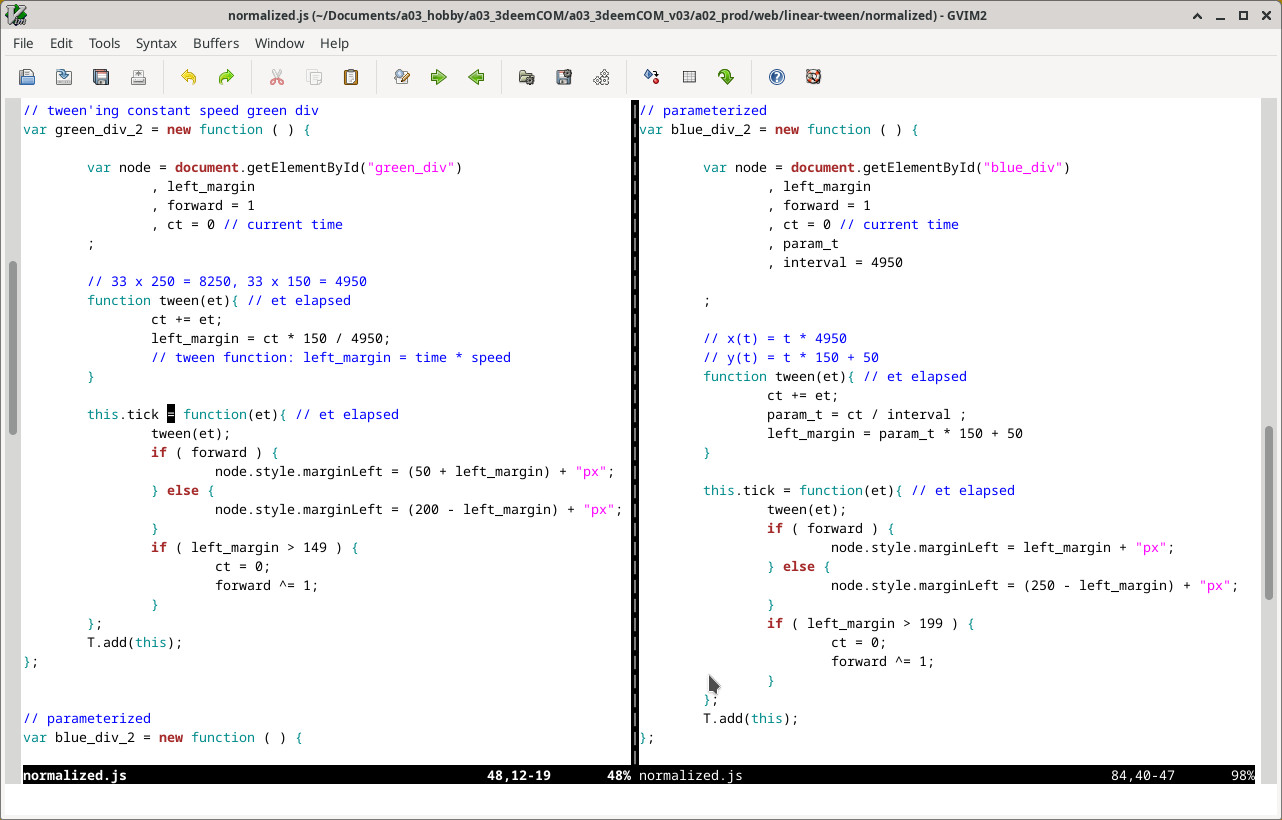
js file link: ./normalized/normalized.js

Conclusion

Normalizing our tween function has the benefit of mapping random end point to 0 to 1. This mapping seems of little benefit as of yet since we are working on a linear tween function. We will see the benefit of mapping to 0 to 1 when we work on an Easing tween function.

Final Notes

Notice that the green and blue not normalized and normalized tween div animations stay in sync. If they didn't, we'd had made an error in our formulations. We expect the red not tween'ed div animation to not stay in sync with the tween'ed ones because of the margin of error in the framerate. Tween'ing accounts for the margin of error.